Các dạng toán bài xích nhì mặt mày phẳng phiu tuy vậy song giải cụ thể được biên soạn bên dưới dạng tệp tin word và PDF bao gồm 2 trang. Các các bạn coi và chuyển vận về ở bên dưới.
Dạng 1. Chứng minh nhì mặt mày phẳng phiu tuy vậy song
Bạn đang xem: Các Dạng Toán Bài Hai Mặt Phẳng Song Song Giải Chi Tiết
1. Phương pháp
Áp dụng thành quả sau:
$\left. \begin{gathered}
a\parallel c,\,\,b\parallel d \hfill \\
a,b \subset \left( Phường \right) \hfill \\
c,d \subset \left( Q \right) \hfill \\
a \cap b = \left\{ A \right\} \hfill \\
\end{gathered} \right\} \Rightarrow \left( Phường \right)\parallel \left( Q \right)$
Áp dụng: Chứng minh đường thẳng liền mạch a tuy vậy song với mặt mày phẳng phiu (P).
$\left. \begin{gathered}
a \subset \left( Q \right) \hfill \\
\left( Q \right)\parallel \left( Phường \right) \hfill \\
\end{gathered} \right\} \Rightarrow a\parallel \left( Phường \right)$
2. Các ví dụ
Ví dụ 1. Cho hình chóp S.ABCD với lòng là hình thang ABCD, $AD\parallel BC,\,\,AD = 2BC$. Gọi E, F, I theo lần lượt là trung điểm của những cạnh SA, AD, SD.
a. Chứng minh $\left( {EFB} \right)\parallel \left( {SCD} \right)$. Từ bại minh chứng $CI\parallel \left( {EFB} \right)$.
b. Tìm gửi gắm tuyến của (SBC) và (SAD). Tìm gửi gắm điểm K của FI với gửi gắm tuyến này, minh chứng $\left( {SBF} \right)\parallel \left( {KCD} \right)$.
Lời giải
a. Ta có:
$EF\parallel SD$ (EF là lối khoảng của tam giác SAD).
$BF\parallel CD$$\left( {BC\parallel FD,\,\,BC = FD} \right)$.
Suy đi ra $\left( {EFB} \right)\parallel \left( {SCD} \right)$.
Mà $CI \subset \left( {SCD} \right)$ nên $CI\parallel \left( {EFB} \right)$.
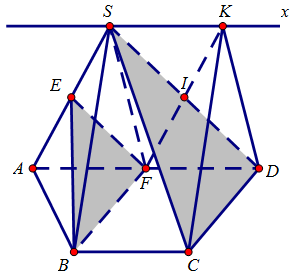
b. Ta có:
$\begin{gathered}
\left. \begin{gathered}
BC\parallel AD \hfill \\
BC \subset \left( {SBC} \right),\,\,AD \subset \left( {SAD} \right) \hfill \\
S \in \left( {SBC} \right) \cap \left( {SAD} \right) \hfill \\
\end{gathered} \right\} \hfill \\
\Rightarrow \left( {SBC} \right) \cap \left( {SAD} \right) = Sx,\,\,Sx\parallel AD\parallel BC \hfill \\
\end{gathered} $
Trong mp(SAD): FI hạn chế Sx bên trên K.
Ta có: $SK\parallel FD,\,\,IS = ID$ nên $IK = IF$.
Vậy tứ giác SKDF là hình bình hành, suy đi ra $SF\parallel KD$.
Mặt không giống $BF\parallel CD$ nên $\left( {SBF} \right)\parallel \left( {KCD} \right)$.
Ví dụ 2. Cho hình chóp S.ABCD, lòng là hình bình hành tâm O. Gọi M và N theo lần lượt là trung điểm của SA và CD.
a. Chứng minh mặt mày phẳng phiu (OMN) và mặt mày phẳng phiu (SBC) tuy vậy song cùng nhau.
b. Giả sử nhì tam giác SAD và ABC đều là tam giác cân nặng bên trên A. Gọi AE và AF theo lần lượt là những lối phân giác nhập của những tam giác ACD và SAB. Chứng minh EF tuy vậy song với mặt mày phẳng phiu (SAD).
Lời giải
a. Ta có:
$ON\parallel BC$ (ON là lối khoảng của tam giác BCD).
$OM\parallel SC$ (OM là lối khoảng của tam giác SAC)
Vì $OM,ON \subset \left( {OMN} \right);\,\,BC,SC \subset \left( {SBC} \right)$ nên $\left( {OMN} \right)\parallel \left( {SBC} \right)$.
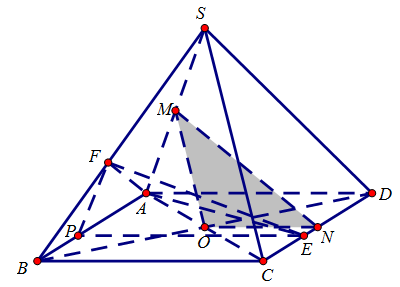
b. Từ E kẻ đường thẳng liền mạch $EP\parallel AD$ (P nằm trong AB) (1)
Khi bại theo dõi đặc thù lối phân giác và tam giác cân nặng tao có:
$\frac{{PB}}{{PA}} = \frac{{EC}}{{ED}} = \frac{{AC}}{{AD}} = \frac{{AB}}{{AS}} = \frac{{FB}}{{FA}}$
Do đó: $PF\parallel SA$ (2)
Từ (1) và (2) suy đi ra $\left( {PEF} \right)\parallel \left( {SAD} \right)$.
Mặt không giống $EF \subset \left( {PEF} \right)$ nên $EF\parallel \left( {SAD} \right)$.
Ngoài đi ra tao hoàn toàn có thể sử dụng tấp tểnh lí Thales nhằm minh chứng $EF\parallel \left( {SAD} \right)$ như sau:
Theo đặc thù lối phân giác và đặc thù của tam giác cân nặng tao minh chứng được:
$\frac{{AB}}{{AS}} = \frac{{AC}}{{AD}} = \frac{{FB}}{{FS}} = \frac{{EC}}{{ED}}$.
Theo tấp tểnh lí Thales tao suy đi ra tía đường thẳng liền mạch BC, EF và SD ở trong tía mặt mày phẳng phiu tuy vậy tuy vậy, suy đi ra EF tuy vậy song với mặt mày phẳng phiu chứa chấp BC và tuy vậy song với mặt mày phẳng phiu chứa chấp SD. Mặt không giống $BC\parallel AD$ nên EF tuy vậy song với mặt mày phẳng phiu (SAD).
Ví dụ 3. Cho hình vỏ hộp ABCD.A’B’C’D’ với những cạnh AA’, BB’, CC’, DD’ tuy vậy song cùng nhau.
a. Chứng minh nhì mặt mày phẳng phiu (BDA’) và (B’D’C) tuy vậy song cùng nhau.
b. Chứng minh rằng lối chéo cánh AC’ trải qua trọng tâm G và G’ theo lần lượt của nhì tam giác BDA’ và B’D’C.
c. Chứng minh G và G’ phân tách đoạn AC’ trở nên tía phần cân nhau.
Lời giải
a. Ta có:
$A’B\parallel D’C$ (vì tứ giác A’BCD’ là hình bình hành).
$BD\parallel B’D’$ (vì tứ giác BB’D’D là hình bình hành), suy đi ra $mp\left( {BDA’} \right)\parallel mp\left( {B’D’C} \right)$.
b. Gọi O, O’ và Q theo lần lượt là tâm những hình bình hành ABCD, A’B’C’D và AA’C’C.
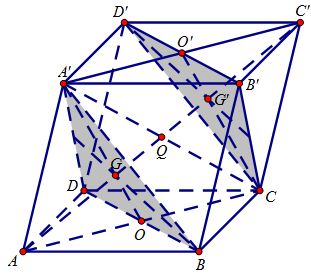
Ta có: A’O là lối trung tuyến và G là trọng tâm của tam giác BDA’ nên $\frac{{A’G}}{{A’O}} = \frac{2}{3}$.
Do bại G cũng chính là trọng tâm tam giác A’AC (vì A’O là lối trung tuyến của tam giác A’AC).
Mà AQ là lối trung tuyến của tam giác A’AC nên G nằm trong AQ, G nằm trong AC’ . (1)
Tương tự động tao với G’ là trọng tâm của tam giác B’D’C và cũng chính là trọng tâm của tam giác A’C’C.
Mà C’Q là lối trung tuyến của tam giác A’C’C nên G’ nằm trong C’Q. Suy đi ra G’ nằm trong AC’. (2)Từ (1) và (2) suy đi ra lối chéo cánh AC’ trải qua nhì trọng tâm G và G’ theo lần lượt của nhì tam giác BDA’ và B’D’C.
c. Ta có:
G là trọng tâm tam giác A’AC nên $\frac{{AG}}{{AQ}} = \frac{2}{3} \Rightarrow \frac{{AG}}{{AC’}} = \frac{1}{3}\,\,\left( {AC’ = 2AQ} \right)$. Suy đi ra $AG = \frac{1}{3}AC’$.
G’ là trọng tâm tam giác A’C’C nên $\frac{{C’G’}}{{C’Q}} = \frac{2}{3} \Rightarrow \frac{{C’G’}}{{C’A}} = \frac{1}{3}\,\,\left( {AC’ = 2C’Q} \right)$. Suy đi ra $C’G’ = \frac{1}{3}AC’$.
Vậy $AG = GG’ = C’G’ = \frac{1}{3}AC’$. Tức là G và G’ phân tách đoạn AC’ trở nên tía phần cân nhau.
Dạng 2. Tìm gửi gắm tuyến của nhì mặt mày phẳng phiu và thám thính tiết diện qua chuyện một điểm và tuy vậy song với một phía phẳng
1. Phương pháp
$\left. \begin{gathered}
\left( Phường \right)\parallel \left( Q \right) \hfill \\
\left( \alpha \right) \cap \left( Phường \right) = a \hfill \\
\left( \alpha \right) \cap \left( Q \right) = b \hfill \\
\end{gathered} \right\} \Rightarrow a\parallel b$
Xem thêm: Đặt vé máy bay đi Quảng Bình giá rẻ nhất tại ABAY.vn
2. Các ví dụ
Ví dụ 1. Cho hình chóp S.ABCD. Gọi M là trung điểm của AD. Gọi $\left( \alpha \right)$ và $\left( \beta \right)$ là mặt mày phẳng phiu qua chuyện điểm M và theo lần lượt tuy vậy song với mặt mày phẳng phiu (SBD) và (SAC).
a. Xác tấp tểnh tiết diện của hình chóp hạn chế vì chưng mp$\left( \alpha \right)$.
b. Xác tấp tểnh tiết diện của hình chóp hạn chế vì chưng mp$\left( \beta \right)$.
c. Gọi H và K theo lần lượt là gửi gắm điểm của $\left( \alpha \right)$ và $\left( \beta \right)$ với AC và BD. Chứng minh tứ giác OHMK là hình bình hành.
Lời giải
a.
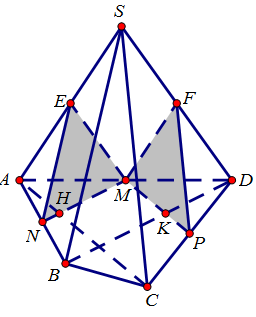
$\left. \begin{gathered}
\left( \alpha \right)\parallel \left( {SBD} \right) \hfill \\
\left( {ABCD} \right) \cap \left( {SBD} \right) = BD \hfill \\
M \in \left( {ABCD} \right) \cap \left( \alpha \right) \hfill \\
\end{gathered} \right\}$
$ \Rightarrow \left( {ABCD} \right) \cap \left( \alpha \right) = MN\parallel BD\,\,\left( {N \in AB} \right)$
Gọi M là trung điểm của AD nên N là trung điểm của AB. Ta có:
$\left. \begin{gathered}
\left( \alpha \right)\parallel \left( {SBD} \right) \hfill \\
\left( {SAB} \right) \cap \left( {SBD} \right) = SB \hfill \\
N \in \left( {SAB} \right) \cap \left( \alpha \right) \hfill \\
\end{gathered} \right\} \Rightarrow \left( {SAB} \right) \cap \left( \alpha \right) = NE\parallel SB\,\,\left( {E \in SA} \right)$
Mà N là trung điểm của AB nên E là trung điểm của SA.
Khi đó: $ME = \left( \alpha \right) \cap \left( {SAD} \right)$.
Vậy tiết diện cần thiết thám thính là tam giác MNE.
b. $\left. \begin{gathered}
\left( \beta \right)\parallel \left( {SAC} \right) \hfill \\
\left( {ABCD} \right) \cap \left( {SAC} \right) = AC \hfill \\
M \in \left( {ABCD} \right) \cap \left( \beta \right) \hfill \\
\end{gathered} \right\} \Rightarrow \left( {ABCD} \right) \cap \left( \beta \right) = MP\parallel AC\,\,\left( {P \in CD} \right)$
Mà M là trung điểm của AD nên Phường là trung điểm của CD.
Ta có:
$\left. \begin{gathered}
\left( \beta \right)\parallel \left( {SAC} \right) \hfill \\
\left( {SCD} \right) \cap \left( {SAC} \right) = SC \hfill \\
P \in \left( {SCD} \right) \cap \left( \beta \right) \hfill \\
\end{gathered} \right\} \Rightarrow \left( {SCD} \right) \cap \left( \beta \right) = PF\parallel SC\,\,\left( {F \in SD} \right)$
Mà Phường là trung điểm của CD nên F là trung điểm của SD.
Vậy tiết diện cần thiết thám thính là tam giác MPF.
c. Trong mp(ABCD): AC hạn chế MN bên trên H, BD hạn chế MP bên trên K. Do MN chứa chấp nhập $mp\left( \alpha \right)$ và MP chứa chấp nhập $mp\left( \beta \right)$ nên H đó là gửi gắm điểm của AC với $mp\left( \alpha \right)$ và K đó là gửi gắm điểm của BD với $mp\left( \beta \right)$.
Ta với $MN\parallel BD$ nên $MH\parallel OK,\,\,MP\parallel AC$ nên $MK\parallel HO$. Vậy tứ giác OHMK là hình bình hành.
Ví dụ 2. Trong mặt mày phẳng phiu (P) cho tới hình bình hành ABCD. Ta dựng những nửa đường thẳng liền mạch tuy vậy song cùng nhau và ở về một phía so với (P) theo lần lượt trải qua những điểm A, B, C, D. Một mặt mày phẳng phiu (P’) hạn chế tứ nửa đường thẳng liền mạch thưa bên trên trên A’, B’, C’, D’. Chứng minh:
a. Tứ giác A’B’C’D’ là hình bình hành.
b. $AA’ + CC’ = BB’ + DD’$.
Lời giải
a. Ta với $AB\parallel CD$ và $Ax\parallel Dt$ nên $mp\left( {Ax,By} \right)\parallel mp\left( {Cz,Dt} \right)$.
Mà $\left( {P’} \right) \cap \left( {Ax,By} \right) = A’B’$; $\left( {P’} \right) \cap \left( {Cz,Dt} \right) = C’D’$ nên $A’B’\parallel C’D’$ (1)
Tương tự:
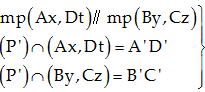$ \Rightarrow A’D’//B’C’$ (2)
Từ (1) và (2) suy đi ra tứ giác A’B’C’D’ là hình bình hành.
b. Gọi O và O’ theo lần lượt là tâm những hình bình hành ABCD và A’B’C’D’.
Khi bại tao với OO’ là lối khoảng của hình thang AA’C’C và hình thang BB’D’D.
Do đó: $AA’ + CC’ = 2OO’$ và $BB’ + DD’ = 2OO’$.
Vậy $AA’ + CC’ = BB’ + DD’$.
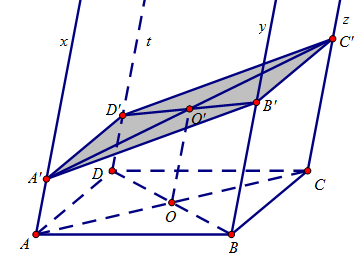
Ví dụ 3. Cho tứ diện ABCD và M, N theo lần lượt là trung điểm của AB, CD. Mặt phẳng phiu $\left( \alpha \right)$ chứa chấp MN hạn chế những cạnh AD và BC theo lần lượt là Phường và Q.
a. Cho trước điểm Phường, hãy thưa cơ hội dựng điểm Q.
b. Gọi K là gửi gắm điểm của MN và PQ. Chứng minh rằng $KP = KQ$.
Lời giải
a. Ta với $\left( \alpha \right)$ là mp(MNP).
Trong mp(ABD): MP hạn chế BD bên trên E.
Trong mp(BCD): EN hạn chế BC bên trên Q.
Vậy $\left( \alpha \right)$ đó là mp(MPNQ). Q là vấn đề cần thiết thám thính.
b. Trên hai tuyến đường trực tiếp chéo cánh nhau AB và CD theo lần lượt với những điểm A, M, B và C, N, D tấp tểnh đi ra những tỉ số vì chưng nhau:
$\frac{{MA}}{{MB}} = \frac{{ND}}{{NC}} = 1$.
Theo tấp tểnh lí Thales tao suy đi ra AD, MN, BC phía trên tía mặt mày phẳng phiu tuy vậy tuy vậy.
Mà PQ là cát tuyến hạn chế tía mặt mày phẳng phiu tuy vậy song theo lần lượt bên trên Phường, K, Q nên: $\frac{{KP}}{{KQ}} = \frac{{MA}}{{MB}} = \frac{{ND}}{{NC}} = 1$.
Vậy K là trung điểm của PQ.
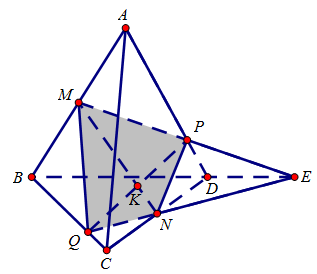
Ví dụ 4. Cho hình chóp $S.ABCD$, với lòng là hình bình hành tâm $O$. Gọi $M,N$ theo lần lượt là trung điểm của $SB$ và $SC$, lấy điểm $P \in SA$.
a) Tìm gửi gắm tuyến $\left( {SAB} \right)$ và $\left( {SCD} \right)$.
b) Tìm gửi gắm điểm $SD$ và $\left( {MNP} \right)$.
c) Tìm tiết diện hình chóp và mặt mày phẳng phiu $\left( {MNP} \right)$. Thiết diện là hình gì?
d) Gọi $J \in MN$. Chứng minh rằng $OJ\parallel \left( {SAD} \right).$
Lời giải
a) Do $AB$ tuy vậy song với $CD$ nên gửi gắm tuyến của $\left( {SAB} \right)$ và $\left( {SCD} \right)$ là đường thẳng liền mạch $d$ trải qua $S$ và tuy vậy song với $AB$ và $CD$.
b) Trong măt phẳng phiu $\left( {SAB} \right)$, kéo dãn $PM$ hạn chế $AB$ bên trên $Q$, nhập mặt mày phẳng phiu $\left( {PMQR} \right)$ , kéo dãn $QN$ hạn chế $SD$ bên trên $R$, gửi gắm điểm của $SD$ và $\left( {MNP} \right)$ là $R$.
c) Thiết diện hình chóp và mặt mày phẳng phiu $\left( {MNP} \right)$ là tứ giác $MPRN$.
Do 3 mặt mày phẳng phiu $\left( {MNP} \right);\left( {ABC} \right);\left( {SAD} \right)$ hạn chế nhau theo dõi 3 gửi gắm tuyến là $PR;MN;AD$ nên bọn chúng tuy vậy song hoặc đồng quy.
Mặt không giống $MN\parallel AD \Rightarrow MN\parallel AD\parallel quảng bá \Rightarrow MPRN$ là hình thang.
Xem thêm: Người bán vé số lời bao nhiêu? Thu nhập trung bình khi bán 100 tờ
d) Ta có: $OM$ là lối khoảng nhập tam giác $SBD$$ \Rightarrow $$OM\parallel SD$.
Tương tự động tao có: $ON\parallel SA \Rightarrow \left( {OMN} \right)\parallel \left( {SAD} \right)$.
Mặt không giống $OJ \subset \left( {OMN} \right) \Rightarrow OJ\parallel \left( {SAD} \right).$(điều cần triệu chứng minh).
Bình luận